מערך הלבק מורכב מחומרי מגנט n52. על ידי סידור מגנטים קבועים עם כיווני מגנט שונים לפי חוק מסוים, הוא מסוגל לרכז את קווי הכוח המגנטיים בצד אחד של המגנט ולהחליש את קווי הכוח המגנטיים בצד השני, כדי לקבל אחד אידיאלי יותר. שדה מגנטי צדדי. יש לכך משמעות רבה בהנדסה, ומערכים של בָּרִיא-ביואיק נמצאים בשימוש נרחב בתחומים תעשייתיים כגון תהודה מגנטית גרעינית, ריחוף מגנטי ומנועים מיוחדים של מגנט קבוע בשל מאפייני הפצת השדה המגנטי המצוינים שלהם.
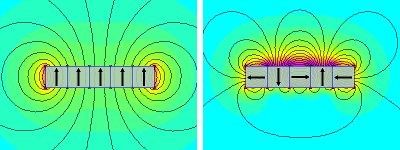
בצד שמאל יש מגנט בודד עם הקוטב הצפוני עד למעלה, וניתן לראות את עוצמת השדה המגנטי בצבעים בתחתית ובראש המגנט. בצד ימין יש מערך הלבק עם שדה מגנטי גבוה יותר בחלק העליון של המגנט וחלש יחסית בתחתית. (חוזק השדה המגנטי של פני השטח החזק של סט מגנטים של מערך הלבק באותו נפח הוא בערך פי 2 (כלומר פי 1.4) מזה של מגנט בודד רגיל, במיוחד כאשר עובי המגנט בכיוון הממגנט הוא בין 4 ו-16 מ"מ.)
טפסים ויישומים של מערך היילבק
1. מערך לינארי
ליניארי היא הצורה הבסיסית ביותר של הרכב מערך הלבך, וניתן לראות את סוג המגנט הזה של מערך כשילוב של מערך רדיאלי ומערך משיק, כפי שמוצג להלן.
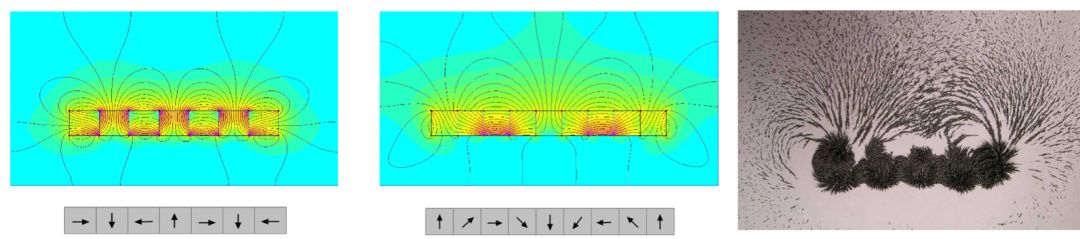
2. מערך מעגלי
ניתן לראות מערך הלבך מעגלי כשילוב של מערכי הלבך ליניאריים הנפגשים ראש אל זנב ויוצרים צורה מעגלית.
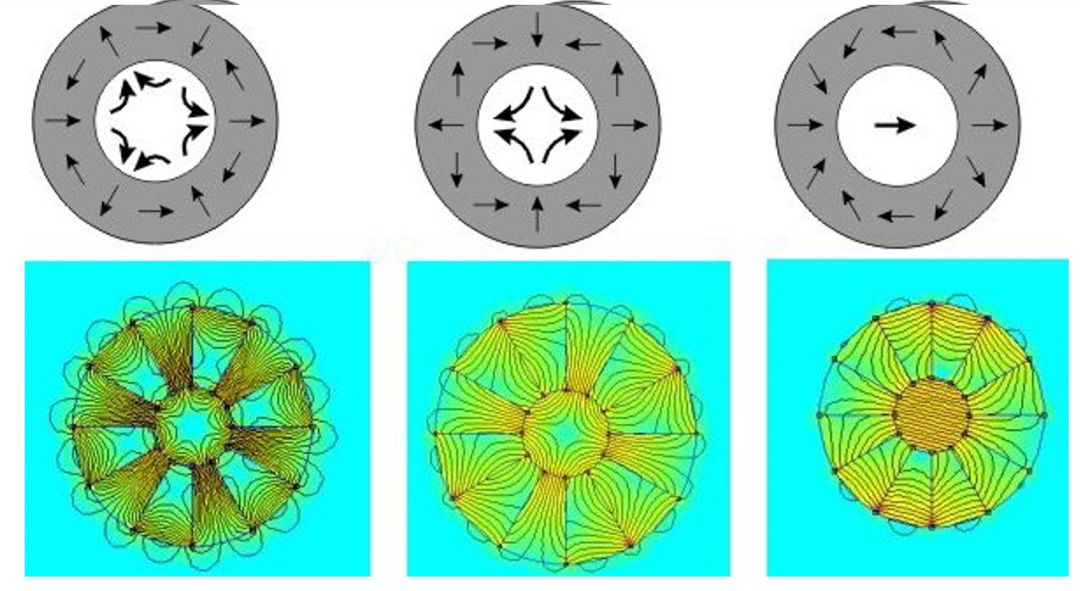
במנועי מגנט קבוע, למנועי מגנט קבוע המשתמשים במבנה מערך הלבך יש שדה מגנטי של מרווח אוויר קרוב יותר לפיזור הסינוסואידי מאשר למנועי מגנט קבוע רגילים, ועם אותה כמות של חומר מגנט קבוע, למנועי מגנט קבוע של הלבך יש צפיפות מגנטית של מרווח אוויר גבוה יותר וברזל נמוך יותר. הֶפסֵד. בנוסף, מערכים מעגליים של הלבך נמצאים בשימוש נרחב במיסבי מגנט קבועים, ציוד קירור מגנטי וציוד תהודה מגנטית.
שיטת ייצור וייצור עבור מערכי יַחנוֹן
שיטה 1:לפי הטופולוגיה של המערך, מקטעי מגנט ממוגנטים מראש מודבקים זה לזה באמצעות דבק מגנט, אותו מהדקים באמצעות תבנית בגלל הדחייה ההדדית החזקה בין מקטעי המגנט. שיטה זו פחות יעילה, אך קלה יותר למימוש ומתאימה יותר למחקר מעבדתי.
שיטה 2:על פי הטופולוגיה של מערכי המגנטים, מקטעי המגנט הממוגנטים מראש מודבקים זה לזה באמצעות דבק מגנט, אשר מהדקים באמצעות תבנית במהלך ההדבקה בגלל הדחייה ההדדית החזקה בין מקטעי המגנט. שיטה זו פחות יעילה אך קלה יותר למימוש ומתאימה יותר לשלב המחקר במעבדה.

שיטה 3:חלוקת שדה מגנטים של היילבק מושגת על ידי שימוש בצורת מערך מפותל ספציפית, כפי שמוצג להלן.
